Все треугольники — равносторонние
(перенаправлено с «Все треугольники - равносторонние»)
Перейти к навигации
Перейти к поиску
Суть софизма[править]
Все треугольники — равносторонние.
Доказательство[править]
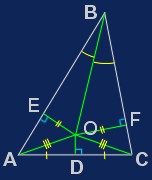
Рассмотрим произвольный . Проведем биссектрису угла B и серединный перпендикуляр к стороне AC; точку их пересечения назовем O. Опустим из нее перпендикуляры EO и OF на стороны AB и BC соответственно.
Так как DO одновременно и высота и медиана , то он равнобедренный и . Так как BO — биссектриса, то, из равенства и (откуда ), . Следовательно, , то есть . Отсюда, так как и , . Проведя такое же рассуждение для основания не AC, а, например, AB, получим, что .
Из этого следует, что все треугольники на свете — равносторонние.
В чём ошибка?[править]
Биссектриса угла и серединный перпендикуляр к противоположной стороне пересекаются за пределами треугольника в неравнобедренном треугольнике и совпадают в равнобедренном.