0=1

Известно много методов доказательства утверждения о равенстве чисел 0 и 1.

Метод степеней единицы

Как известно, $1^{a}=1$, таким образом, Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle 1^{1}=1^{0}=1} . Но, если равны основания степеней и их значения, то равны и показатели, то есть $0=1$, что и требовалось доказать.

Метод умножения

Справедливо равенство Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle 0*0=0*1} . Поделим это выражение на $0$. Получим: Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle {\frac {0}{0}}\cdot 0={\frac {0}{0}}\cdot 1} , отсюда выходит, что $0=1$.

Но есть одна загвоздка: на 0 делить нельзя.

Упрощённый метод умножения

Дано: $0\cdot 0=0\cdot 1$. Так как $0=0$, то $0=1$.

Факториальный метод

Обычно факториалы разных чисел имеют разное значение. Однако Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle 0!=1} и Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle 1!=1} , то есть Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle 0!=1!} . Ссылаясь на ранее написанное, можно сказать, что $0=1$.

Метод вынесения множителей

Справедливо равенство Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle 2:2=3:3} . Вынесем общий множитель: Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle 2(1:1)=3(1:1)} . Сократим: Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle 2=3} . Вычтем 2 и получим искомое равенство.

Метод деления

Допустим, что есть некое равенство Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle a-b=0} . А теперь поделим каждую сторону на $a-b$. Получим: ${\frac {a-b}{a-b}}={\frac {0}{a-b}}$, или $1=0$.

Метод логарифмирования

Согласно формулам, Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle log_{a}a=1} и Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle log_{a}1=0} . Подставим Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle a=1} . Получим: из первой формулы Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle log_{1}1=1} , но из второй формулы $log_{1}1=0$. Это значит, что $0=1$, что требовалось доказать.

Тригонометрический метод 1

$sin0=sin\pi$, отсюда вытекает, что $0=\pi$, Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle 0\pi =1\pi } , а это значит, что $0=1$, что и требовалось доказать.

Тригонометрический метод 2

Метод, подобный предыдущему. Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle tg0=tg\pi } , значит, $0=\pi$, Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle 0\pi =1\pi } , и в конце концов $0=1$.

Тригонометрический метод 3

Метод, напоминающий два предыдущих. Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle cosec0=cosec\pi } , таким образом, $0=\pi$, или Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle 0\pi =1\pi } , откуда вытекает искомое равенство $0=1$.

Тригонометрический метод 4

Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle cos{\frac {\pi }{2}}=cos{\frac {3\pi }{2}}} , следственно Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle {\frac {\pi }{2}}={\frac {3\pi }{2}}} , Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle 3=2} , откуда выходит, что $0=1$.

Тригонометрический метод 5

Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle ctg{\frac {\pi }{2}}=ctg{\frac {3\pi }{2}}} , значит, Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle {\frac {\pi }{2}}={\frac {3\pi }{2}}} , Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle 3=2} и $0=1$, что и требовалось доказать.

Тригонометрический метод 6

Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle sec{\frac {\pi }{2}}=sec{\frac {3\pi }{2}}} , таким образом получаем, что Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle {\frac {\pi }{2}}={\frac {3\pi }{2}}} , Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle 3=2} , следственно,$0=1$.

Тригонометрический метод 7

$sin{\frac {\pi }{4}}=cos{\frac {\pi }{4}}$, откуда можно предположить, что Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle sin0=cos0} , значит, $0=1$.

Тригонометрический метод 8

$sin{\frac {\pi }{4}}=cos{\frac {\pi }{4}}$, следственно, Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle sin{\frac {\pi }{2}}=cos{\frac {\pi }{2}}} , и, таким образом, $0=1$, что и следовало доказать.

Метод производных

Как известно, Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle x'=1} при любом $x$. Но, подставив вместо $x$, получаем, что производная становится равной 0. Следственно, $0=1$.

Алгебраический метод

Рассмотрим равенство $a=b+c$. Умножим обе его части на $a-b$. Получим: $a^{2}-ab=ab+ac-b^{2}-bc$, то есть $a^{2}-ab-ac=ab-b^{2}-bc$. Разложим на множители, получим Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle a(a-b-c)=b(a-b-c)} , сокращаем, получаем $a=b$. То есть, подставив Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle a=1} , $b=0$, получим требуемое равенство. Впрочем, этот метод годится для доказательства равенства всех чисел.

Иррациональный метод

Докажем сначала, что Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle 1=-1} . Понятно, что ${\sqrt {-1}}={\sqrt {-1}}$. Представим в левой части равенства $-1={\frac {-1}{1}}$, а в правой Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle -1={\frac {1}{-1}}} . Получим ${\sqrt {\frac {-1}{1}}}={\sqrt {\frac {1}{-1}}}$. Известно, что корень из дроби есть корень из числителя делённый на корень из знаменателя. Поэтому Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle {\frac {\sqrt {-1}}{\sqrt {1}}}={\frac {\sqrt {1}}{\sqrt {-1}}}} . По свойству пропорции: ${\sqrt {-1}}\cdot {\sqrt {-1}}={\sqrt {1}}\cdot {\sqrt {1}}$. Следовательно, Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle -1=1} . Прибавив к обеим частям равенства 1 и разделив их на 2, получим требуемое равенство $0=1$.

Геометрический метод 1

Равные треугольники

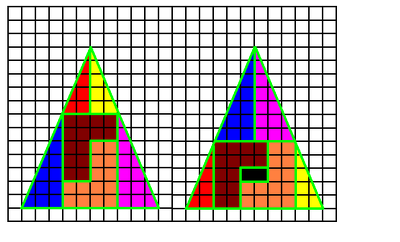
Рассмотрим два треугольника, представленных на рисунке. Площадь первого треугольника равна 60 клеточкам, а площадь второго треугольника, составленного из тех же фигур, что и первый треугольник, равна 58 клеточкам (две чёрные клетки внутри вырезаны). Получается, что Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle 58=60} . Отнимем от обеих частей равенства 58 и разделим на 2, получим Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle {\frac {58-58}{2}}={\frac {60-58}{2}}} , то есть $0=1$, что и требовалось доказать.

Метод бесконечных рядов

Докажем, что Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle 1=-1} , только иначе.

Рассмотрим сумму бесконечного ряда Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle S=1+1-1+1-1+1-1...} . Представим её в виде Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle S=1+(1-1)+(1-1)+(1-1)...=1+0+0+0...=1} . Теперь представим S теми же слагаемыми, но начиная с последнего. Имеем Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle S=-1+1-1+1-1+1-1=-1+(1-1)+(1-1)+(1-1)=-1+0+0+0=-1} , то есть Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle S=1=-1} , значит Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle 1=-1} , откуда, как доказано выше, вытекает, что $1=0$.

Метод мнимых единиц

Метод, предложенный канадскими учёными. Понятно, что Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle {\frac {-1}{1}}={\frac {1}{-1}}} . Значит, ${\sqrt {\frac {-1}{1}}}={\sqrt {\frac {1}{-1}}}$. Значит, Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle {\frac {\sqrt {-1}}{\sqrt {1}}}={\frac {\sqrt {1}}{\sqrt {-1}}}} . Так как ${\sqrt {-1}}=i$, запишем равенство следующим образом: Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle {\frac {i}{1}}={\frac {1}{i}}} . Разделим обе части на 2, получим Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle {\frac {i}{2}}={\frac {1}{2i}}} . Далее, прибавим к обеим частям равенства выражение Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle {\frac {3}{2i}}} , получим Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle {\frac {i}{2}}+{\frac {3}{2i}}={\frac {1}{2i}}+{\frac {3}{2i}}} . Теперь умножим обе части на $i$, получим Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle i({\frac {i}{2}}+{\frac {3}{2i}})=i({\frac {1}{2i}}+{\frac {3}{2i}})} , раскроем скобки: ${\frac {i^{2}}{2}}+{\frac {3i}{2i}}={\frac {i}{2i}}+{\frac {3i}{2i}}$. Так как Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle i^2=-1} , получаем Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle {\frac {-1}{2}}+{\frac {3}{2}}={\frac {1}{2}}+{\frac {3}{2}}} . Посчитав, получим, что Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 1=2} , а отняв Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 1} , найдем требуемое равенство: Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=1} .